By Factor theorem, we can say that (x−1) is the factor of p(x)= x 3 −2 x 2 −x2 We can also find other factors of p(x) by doing long division but we will just split theAlgebra Factor (xy)^3 (xy)^3 (x y)3 − (x − y)3 ( x y) 3 ( x y) 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = xy a = x y and b = x− y b = x yNCERT Solutions NCERT Solutions For Class 12 NCERT Solutions For Class 12 Physics

Solved Solve The Following Using Separation Of Variables A Chegg Com
(x y)^3-(x^3 y^3) factorise
(x y)^3-(x^3 y^3) factorise- factorise the following a) (xy) 3 (yz) 3 (zx) 3 b) 25x 2 16y 2 4z 2 40xy16yz zx c) 1 64x 3 d) 2root2a 3 8b 3 27c 3 18root2 abc e) 842rSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community
Algebra Polynomials and Factoring Factoring Completely 1 Answer Konstantinos Michailidis It is x3 y3 z3 −3xyz = x3 y3 3x2y 3xy2 z3 − 3xyz − 3x2y − 3xy2 = (x y)3 z3 − 3xy(x y z) = (x y z)((x y)2 z2 −(x y)z) −3xy(x y z) = (x y z)(x2 2xy y2 z2 −xy −xz − 3xy) = (x y z)(x2 y2Rewrite 64x^{3}y^{6} as \left(4x\right)^{3}\left(y^{2}\right)^{3} The difference of cubes can be factored using the rule a^{3}b^{3}=\left(ab\right)\left(a^{2Factor (xy)^3 (xy)^3 (x y)3 (x − y)3 ( x y) 3 ( x y) 3 Since both terms are perfect cubes, factor using the sum of cubes formula, a3 b3 = (ab)(a2 −abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x y a = x y and b = x− y b = x y
Find an answer to your question (xy)3 (xy)3 can be factorized as kartikey kartikey Math Secondary School answered (xy)3 (xy)3 can be factorized as 1 See answer Advertisement Advertisement kartikey is waiting for your help Add your answer and earn points FinesisQ 3 Find what the following equations become when the origin is shifted to the point (1,1)?Tap for more steps Factor x x out of x 3 x 3 Factor x x out of − 4 x 4 x Factor x x out of x ⋅ x 2 x ⋅ − 4 x ⋅ x 2 x ⋅ 4 Rewrite 4 4 as 22 2 2 Factor
Answer (1 of 9) Whenever a teacher gave me something like this, I would use a trick I called derive and divide Here's my recipe 1 Derive the polynomial until you're smart enough to factor it out 2 Take the terms that are left one by one and do an algebraic division 3 Repeat Here it goePREMISES f= (xy)^3–8 (xy)^3 in factored form ASSUMPTIONS Let z=the expansion of the polynomial (xy)^3–8 (xy)^3 Let f=the factorization (simplification) of the polynomial (xy)^3–8 (xy)^3 EXPANSION z= (xy)^3–8 (xy)^3 (Rewrite the expression inAnswer (1 of 10) This will go according to the formula a^3b^3=(ab)(a^2abb^2) So the solution for the mentioned problem goes like this, the above equation will be converted to the mentioned form a^3b^3 3√3x^3y^3 3=√3*√3=√3^2=3 √3*√3*√3x^3y^3 (√3x) ^3y^3 (√3xy)((√3x^2)√3xyy^2) (√




Math Problem Factorization X 4y X 2y 3 X 3y 2 Xy 4 Youtube




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
Question factor x^3y^3 into irreducibles in Q(x,y) and prove that each of the factors is irreducible Answer by richard1234(7193) (Show Source) You can put this solution on YOUR website! x^3 y^3 = (x y)(x^2 xy y^2) Algebra Science How do you factor #x^38y^3#?Factorise the following by using suitable identity x26xy9y2 Mathematics Q 5 Factorise 6xy9y2 Mathematics Concise Mathematics Standard VIII Q 1 Factorise Completely x 2 − y 2 − 3 x − 3 y Mathematics RS Agarwal Standard IX




Factorise 8 X Y 3 Z 3 Brainly In



Solved Find The General Solution Of The Differential Equation 3 Y X 2 2 X Y Y 3 D X X 2 Y 2 D Y 0 Course Hero
Join this channel to get access to perkshttps//wwwyoutubecom/channel/UCFhqELShDKKPv0JRCDQgFoQ/joinHere is the technique to find the area under 3 curves aIn the expression, if we replace y with (− y), we will get the identity x 3 − y 3 Now, let's further verify this numerically with an example To verify, let's take the values for x and y and put in the LHS and RHS of the identityWe know the corollary if a b c = 0 then a 3 b 3 c 3 = 3 a b c Using the above identity taking a = x − y , b = y − z and c = z − x , we have a b c = x − y y − z z − x = 0 then the equation ( x − y ) 3 ( y − z ) 3 ( z − x ) 3 can be factorised as follows




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Example 25 Factorise 8x3 Y3 27z3 18xyz Class 9
Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)3x^5y 27x^4y^212x^3y^3 =3x^3y(x^2 9xy4y^2) BYJU'S Answer; What are the factors of ( xy)3(x3y3) pp pp Math Secondary School answered What are the factors of ( xy)3(x3y3) 2 See answers Advertisement Advertisement madhura madhura ⬆️⬆️⬆️Hope This Helps u☺ Advertisement Advertisement




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Factorise 8 X Y 3 27 X Y 3
Factorise (x y) 3 8x 3 Factorise fully x^3x Question 1 (2 points) An opentop box is formed by cutting squares out of a 5 inch by 7 inch piece of paper and then folding up the sidesFactor x^3 3x^2 x 3




Expert Answer What Are The Factors Of X Y 3 X3 Y3 Brainly In



How To Factor X 3 X 2 Xy X Y 1 Quora
View Full Answer Deep Sah, added an answer, on 3/10/15 Deep Sah answered this We know that a^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab bc ac) Take, a = xy, b = yz, c = zx we get, (xy)^3 (yz)^3 (zx)^3 3 (xy) (yz) (zx)Factoring » Tips for entering queries Enter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask about factoring factor quadratic x^27x12; Find the value of k,if y3 is a factor of 3y(to the power square) ky 6 asked in Class IX Maths by muskan15 Expert ( 379k points) polynomials




Factorizing If 2x 1 Is A Factor Of The Expression 6 X2 5x



Solved Supply Solution To 3 X 2 Y 2 X Y Y 3 D X X 2 Y 2 D Y 0 Through Determination Of Integrating Factors Course Hero
How do you factor # x^3 1#?Xy is obviously irreducible For sake of completeness, we show that x^2 xy y^2 is irreducible Suppose that, on the contrary, it is reducible34 Luego de factorizar el polinomio ( ) 3 3 3 2 2 2 2 2 2 x;y;z R x y z x y y z z x xy yz zx = , indique un factor primo A) x yz B) xy z C) x y z D) 2 2x y z E) 2 2x y z 35




Solved Solve The Following Using Separation Of Variables A Chegg Com




Factorize 27 X Y 8 2x Y Brainly In
Expand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!X (xy)^33x^2y (xy)factorise it in a cup there is a mixture with 3 parts of milk and 1 part of water the part of the cup filled with water is?step explanation Add the following fractions 3/41/3 find the equation of the circles which touch both the axes and touch the line x=2a 19A certain car loses 50% of its value each year




Solving A Quadratic Equation By Factoring A Plus Topper




Factorise X Y 2x 5 X Y X 3 Maths Factorisation Meritnation Com
See all questions in Special Products of Polynomials Impact of this question 6635 views around the world You How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Factor x^3y^3 x3 − y3 x 3 y 3 since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)what i hope to do in this video is prove the angle addition formula for sine or inSubtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0 Reorder the terms Reorder the terms This is true for any x This is true for any x Use the distributive property to multiply xy by x^




Factorize X 3y 3 3x Y 3 Brainly In




Solved Find The Special Integrating Factor To Make The Given Chegg Com
Factorisea 33a 2b3ab 2b 3−8 Factorize the following quadratic polynomial by using the method of completing the square 4y 212y5 Factorize the following algebraic expression a 2 − b 2 2 b c c 2 Resolve the following quadratic trinomial into factor 3 x 2 1 0 x 3(i) x2xy−3y2−y2=0 (ii) xy−y2−xy=0 (iii) xy−x−y1=0 (iv) x2−y2−2x2y=0 Mathematics Q 4 Factorise y2−1−2x−x2 Maths Q 5 The coordinates of the radical centre of three circles x2y22x3y1=0, x2y2xy2=0,x2y23x2y1=0 Ex 25, 9Verify (i) x3 y3 = (x y) (x2 – xy y2)LHS x3 y3We know (x y)3 = x3 y3 3xy (x y)So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy




Without Finding The Cubes Factorise X Y 3 Y Z 3 Z X 3 Maths Polynomials Meritnation Com




Bestpixtajpm1d3 ダウンロード済み Factorise X X 3 Y 3 3xy X Y
X3y3=152 No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation x^3y^3(152)=0 Step We can write this expression as x3 − (2y)3 The formula for factorizing the Difference of two Cubes is a3 −b3 = (a −b)(a2 ab b2) In x3 −(2y)3, a = x b = 2y x3 −(2y)3 = (x −2y) ⋅ (x2 (x ⋅ 2y) (2y)2)Expand x^3 y^3 z^3 plot x^3 y^3 z^3 factor x^3 y^3 z^3 complex




Factorise X Cube Minus 2 X Square Y 3 X Y Square Minus 6y Cube Brainly In




Factoring Special Binomials
Step 1 Each term of given algebraic expression is written as a product of irreducible factors Step 2 The common factors are taken out and the rest of the expression is combined in the brackets For example 1 Factorise 6xy 15yz Step 1 we have, 6xy = 2 × 3 × x × y 15yz = 3 × 5 × y × z Step 2 Common factors of these terms are 3 and yAnswer (1 of 5) At first glance (0,1) and (1,0) are solutions If it has a nice linear solution, fitting this then that would be y= x1, lets plug it in x^3 3x(x1) (x1)^3 1 = x^ 3x^2 3x 1 x^2 3x^2–3x1–1=0 Well, then lets try to factor out yx1 using the usual polynomial divis Factor x 4 y 2 x 3 y 3




8 X Y 3 27 X Y 3 Pleaser Factorise This Maths Polynomials Meritnation Com




Factoring Two Variable Quadratics Rearranging Video Khan Academy
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Factorcalculator factorizar x^{3}y^{3} zs Related Symbolab blog posts Middle School Math Solutions – Polynomials Calculator, Factoring Quadratics Just like numbers have factors (2×3=6), expressions have factors ((x2)(x3)=x^25x6) Factoring is the process This is a semiimportant identity to know (x^3y^3)=(xy)(x^2xyy^2) Although it doesn't apply directly to this question, it's also important to know that (x^3y^3)=(xy)(x^2xyy^2) This gives us the rule (x^3y^3)=(xy)(x^2∓xyy^2)




X 3 Y 3 X 3 Y 3 Formula Proof Youtube




Solved Simplify 64 X X Y 3 2 Express In Scientific Chegg Com
Y=x3x24x4 No solutions found Reformatting the input Changes made to your input should not affect the solution (1) "x2" was replaced by "x^2"Factor (xy)^23(yx)^3 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps factorise (xy)3(yz)3(zx)3 Maths Polynomials NCERT Solutions;



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community




Factorise X X Y 2 3x2y X Y Maths Polynomials Meritnation Com
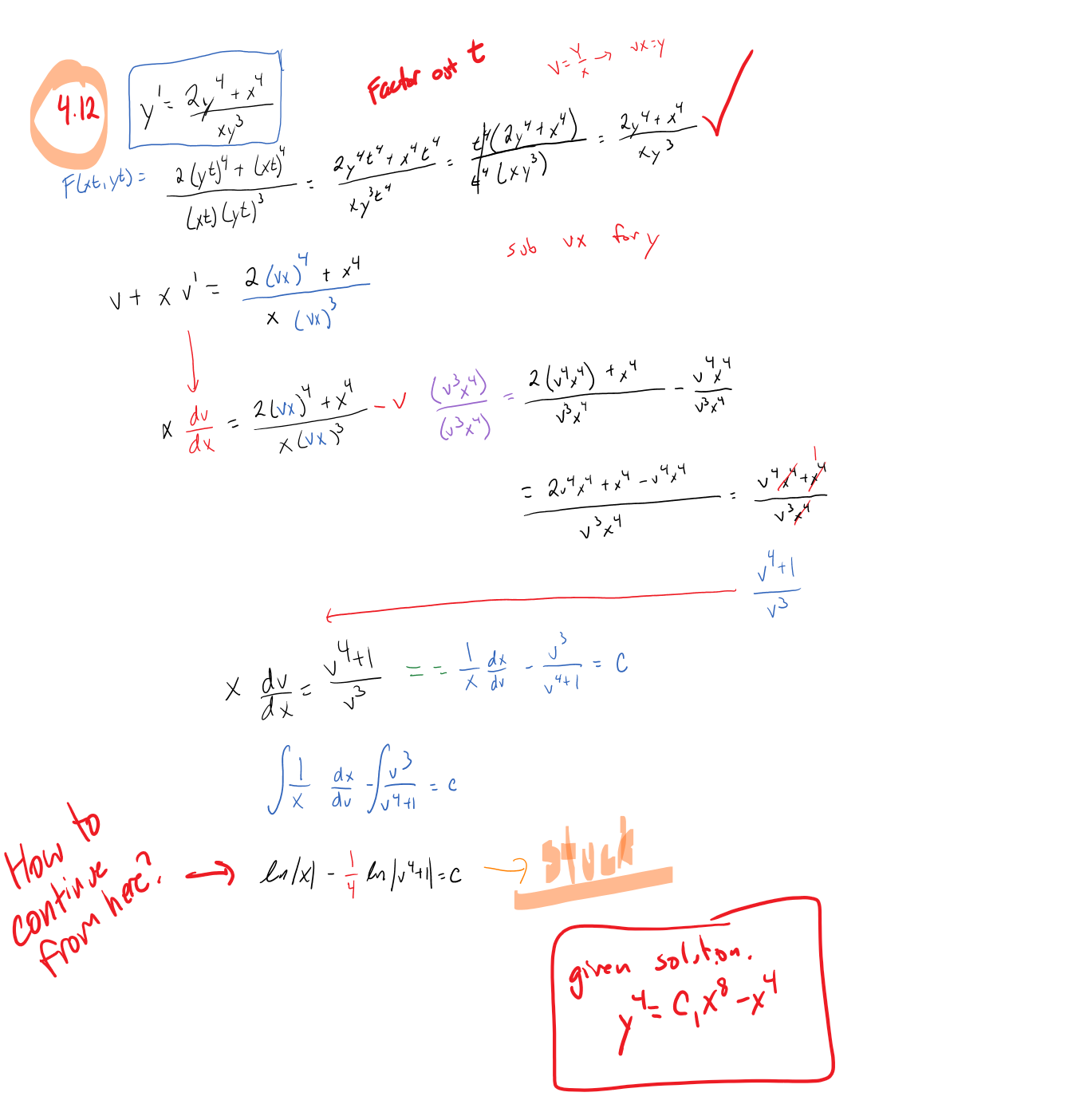



Solved Solve Y 2 Y4 X 4 Xy 3 I Am Stuck On The Chegg Com




Learn Algebraic Identities Of X Y And X Y In 3 Minutes



Factorisation Factorise X Y 3 X Y 3 Factorise X Y 3 X Y 3 Factorisation Class 9 Youtube




Solved Let F X Y X 3 3xy 2 2y 3 Show That The Chegg Com




Factor X 4 Xy 3 X 3 Y 3 Out Completely Hint First Factor Out A Monomial Brainly Com



How To Solve This Differential Equation X 2 Y X 3dy Dx Y 4cosx Quora



Factorise The Expression X Y Z 3 X 3 Y 3 Z 3 Into Linear Factors Youtube



Maths X 3013b Factorization Factorise X 3 Y 3 6xy 8 And X 3 8y 3 1 6xy Youtube




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation




Factorizing If 2x 1 Is A Factor Of The Expression 6 X2 5x



Factoring By Regrouping




Factorize X 3 Y 3 3 X Y 1 Nfactorise Cdot X 3 64 Y 3 8 Z 3




Factorise Br Y 2 Xy 1 X X 3




Factorise X X 3 3 3x 2y X Y Brainly In




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation




5 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Fa Ctors Brainly In




Example 3 Standardized Test Practice Solution 8x 3 Y 2x Y 2 7x4y37x4y3 4y4y 56x 7 Y 4 8xy 3 Multiply Numerators And Denominators 8 7 X X 6 Y 3 Y 8 X Ppt Download




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




Factorise X 3 27y 3 8z 3 18xyz




Which Of The Following Is A Factor Of X Y 3 X 3 Y 3




Factorise 64 X Y 3 125 2x Y 3 Maths Factorisation Meritnation Com




Factorisation Factorise X Y 3 X Y 3 Factorise X Y 3 X Y 3 Factorisation Class 9 Youtube




Solved A 12 Solve The Following Initial Value Problems Chegg Com




Factorise 8 X Y 3 27 X Y 3 Brainly In




Factorize 8 X Y 3 27 X Y 3 Youtube




Factoring And The Factor Theorem Hints To Determine Each Type Ppt Download




5 5 Factoring The Sum And Difference Of Two Cubes Ppt Download



Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube



If X Y Y X 1 Find The Value Of X 3 Y 3



X3 Y3 Identity



How To Factorise 3 X Y 2 2 X Y Quora



What Is The Completely Factored Form Of Xy3 X3y The 3 S Are Po




What Are The Factors Of X Y 3 X 3 Y 3 Maths Polynomials Meritnation Com




Factoring Calculator Wolfram Alpha



Factoring And The Factor Theorem Hints To Determine Each Type Ppt Download




Factorise X Y 3 X 3 Y 3 3xy X Y Brainly In




Which Of The Following Is A Factor Of X Y 3 X 3 Y 3




Q27 Q27 X Y 3 X Y 3 Can Be Factorized As Maths Polynomials Meritnation Com



1




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Solved Separating The Varia Bles I 1 Xy 3 Dx 4y Dy Dx 2 Chegg Com




Math 432 Hw 2 5 Solutions




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Factorise X Y 3 8x 3 Brainly In




Copyright C Cengage Learning All Rights Reserved Factoring Polynomials And Solving Equations By Factoring Ppt Download



One Of The Factors Of 25x 2 1 1 5x 2 Is



8p3 Q3 2p 3 Q 3 A3 And We Have A Difference 2p Q 2p 2 2p Q
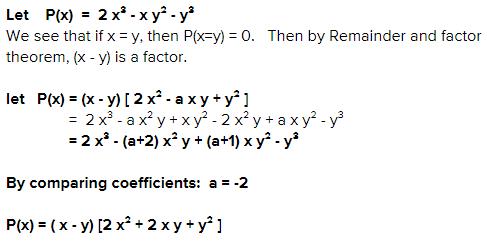



Factorise 2x 3 Xy 2 Y 3 Edurev Class 9 Question




Please Quickly Answer Factorise 2x 3 Xy 2 Y 3 Maths Polynomials Meritnation Com




X 2 Xy 4 Dx 2y 3dy 0 Mathematics Stack Exchange




Rd Sharma Solutions For Class 9 Maths Chapter 5 Factorization Of Algebraic Expressions Updated For 21 22




Factorise 27 X Y 3 8 X Y 3 Maths Polynomials Meritnation Com




Factorise X Y 3 X Y Brainly In




Factorise X 3 Y 3 Xy X Y
.png)



Factorise X3 Y3 Maths Polynomials Meritnation Com




Factorise X3 9y3 3xy X Y Brainly In




Solved Solve The Differential Equation Using Integrating Chegg Com




Factorize X X Y 3 3x 2y X Y




Ex 14 2 3 Iii Factorise 2x 3 2xy 2 2xz 2 Ex 14 2




Solved 3x Xy 2 Dx X 3 2y Dy 0 Y 0 2 Dy Dx Chegg Com




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




How To Factor Binomials Factoring Checklist I Binomials
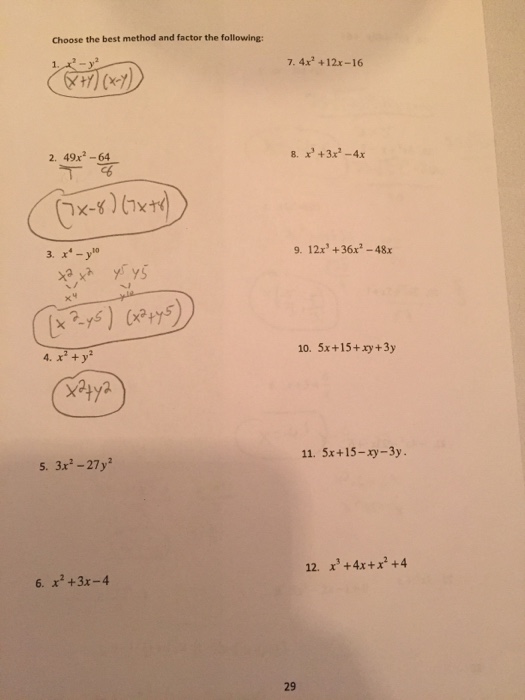



Solved Choose The Best Method And Factor The Following Chegg Com




Chapter 6 Review Factor The Expression 1 6x 3 2 X3 4x2 3 4z



An Integrating Factor Of The Differential Equation Y 4 2y Dx Xy 3 2y 4 4x Dy 0 Is Snapsolve




Q 3 Find The Integrating Factor And Solve The Exact Solution Consider The Differential Equation E X Y Cosy Cosx 2e 2x Y Dx Sinx E X Y Siny 3y 2e Y Dy Q 5 Prove Socratic




Factorise X 5 Y 5




Without Finding The Cubes Factorise X Y 3 Y Z 3 Z X 3 Brainly In




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube



Factorise X X Y 3 3x2y X Mathematics Topperlearning Com




Factorise 8 X Y 3 27 X Y 3 Maths Polynomials Meritnation Com




2 Math With Jm Home




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Solved Factor Completely 3y 3 12x 2 Y 7a 3 7 X 3 Chegg Com



0 件のコメント:
コメントを投稿